In this blog post we're coming back to indexed sequence CRDTs - we already discussed some operation-based approaches in the past. This time we'll cover YATA (Yet Another Transformation Approach): a delta-state based variant, introduced and popularized by Yjs framework used to build collaborative documents.
If you're not familiar with topic of Conflict-free Replicated Data Types, you can start learning about them here.
Foundations of indexed collection CRDTs
A specific property of indexed CRDT collection is that - unlike sets or maps, which only define presence/absence of an element - they allow us to define insert/delete operations using arbitrary order: a property that's especially vital for use cases like collaborative text editing. We already discussed two different indexed sequence CRDTs on this blog: LSeq and RGA. Now it's a time for YATA.
A core concept behind all indexed CRDTs is notion of unique identifier assigned to the inserted element - I referred to it as a virtual pointer in the past blog posts - which allows us to track the position of that element while its actual index (as observed by user) may change whenever other elements in a collection come and go.
A popular approach is to define that unique identifier as a composite of two values:
- Sequence number used for comparison. It varies depending on the algorithm:
- LSeq uses a variable-length byte sequence which is a function
id(left_neighbor, righ_neighbor)that's expected to produce a sequence which is lexically greater than id of an item at previous index, but lower than id of an item at the next index (lseq[n-1].id < lseq[n].id < lseq[n+1].id). - RGA maintains a single globally incremented counter (which can be ordinary integer value), that's updated anytime we detect that remote insert has an id with sequence number higher that local counter. Therefore every time, we produce a new insert operation, we give it a highest counter value known at the time.
- YATA also uses a single integer value, however unlike in case of RGA we don't use a single counter shared with other replicas, but rather let each peer keep its own, which is incremented monotonically only by that peer. Since increments are monotonic, we can also use them to detect missing operations eg. updates marked as
A:1andA:3imply, that there must be another (potentially missing) updateA:2.
- LSeq uses a variable-length byte sequence which is a function
- Unique identifier of a given replica/peer. Since we cannot guarantee uniqueness of sequence numbers generated concurrently by different peers, we can use them together with peer's own ID to make it so.
With these in hand we are not only able to identify each inserted element uniquely (no matter who and when assigned insert request), but also to compare them in a deterministic manner: which may be necessary when i.e. two peers will insert two different items at the same index without talking with each other.
Interleaving
We already discussed interleaving issue in the past, but lets quickly remind it here together with the ways on how to avoid it.
In short interleaving may happen, when two peers decide to insert entire ranges of elements at the same index. After synchronizing with each other it may turn out that their inserts are mixed (interleaved with each other). While this may not be an issue in some cases, there's a one famous scenario where this behavior wrecks havoc: collaborative text editing.
Two people, Alice and Bob, want to collaborate over a text document. Initial document content was "hi !". While offline, Alice edited it to "hi mom!", while Bob to "hi dad!". Once they got online, their changes were synchronized. What's a desired state of the document after sync?
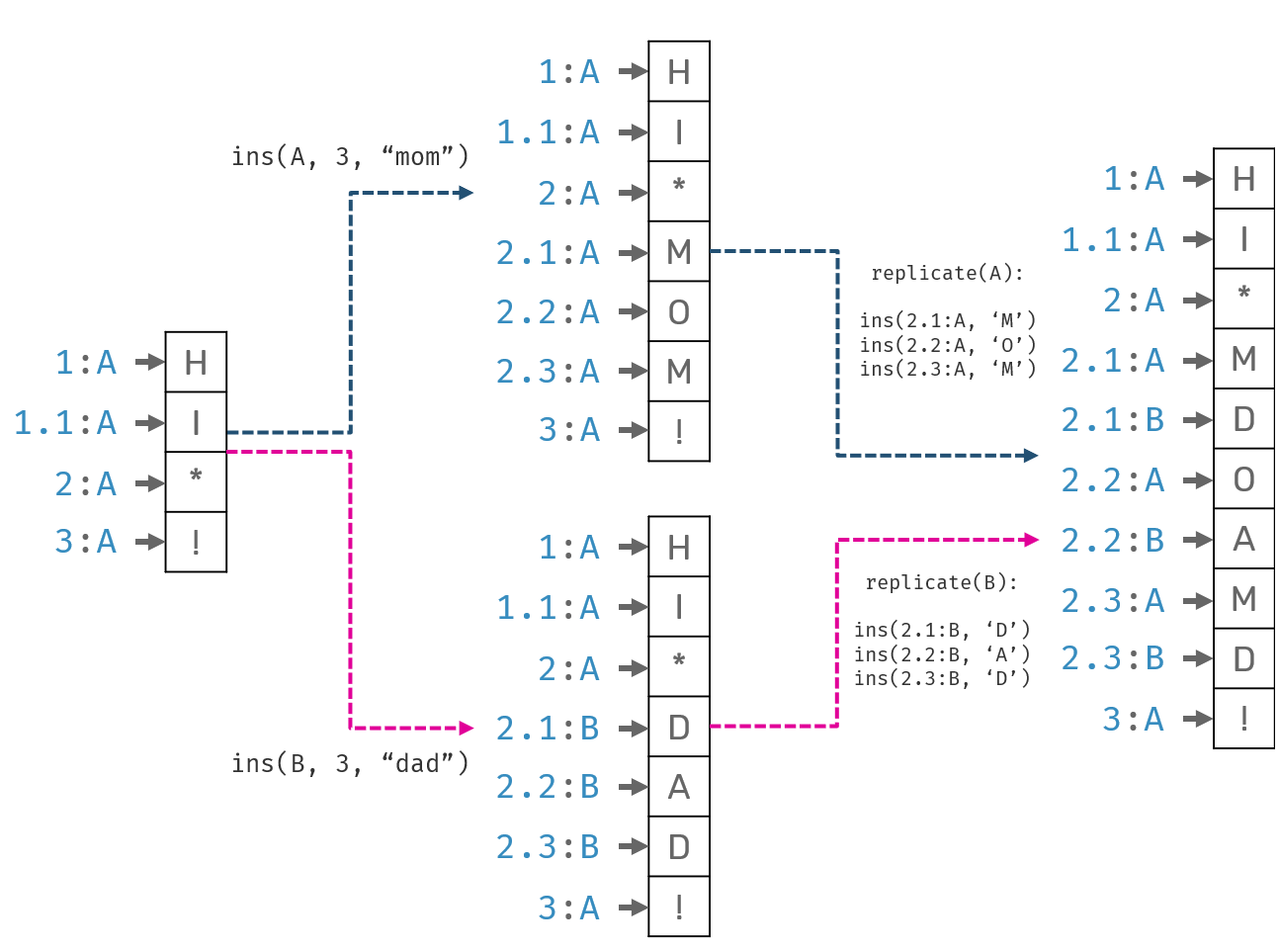
While we could accept resolved document in form of "hi momdad!" or "hi dadmom!" - since they are easy to fix - the fact that characters from individual users could be mixed together would result in subpar user experience.
Mitigating interleaving issues
Interleaving was especially prevalent issue of a LSeq algorithm. But why? The reason for this is as always: we didn't provide enough metadata to preserve the intent in the face of concurrent updates - in this case placing series of characters one right after another.
If we define each LSeq insert operation as ins(id, char), we can try to represent "abc" as series of inserts [ins(1:A, 'a'), ins(2:A, 'b'), ins(3:A, 'c')]. These however are not equivalent: we just defined 3 operations that look like they are independent on each other. If our intent was to represent them one after another, we didn't have a way to specify it.
RGA solved problem of interleaving by attaching a predecessor as a part of operation eg. ins(predecessor, id, char). This way we can define "abc" as [ins(<root>, 1:A, 'a'), ins(1:A, 2:A, 'b'), ins(2:A, 3:A, 'c')], and preserve information about the dependency chain between these characters. Does that mean that RGA solved the interleaving issue? There are corner cases where interleaving can still happen - like inserting at the start of a list or in the case of prepends (since we only defined predecessor/left neighbor of an element).
YATA is similar to RGA in regard to keeping expected predecessor id as part of the operation. Additionally we also attach a successor id. In YATA naming convention, we call them left/right origins. Therefore insert operation can be defined as ins(left, right, id, char). Why do we need two origins instead of one like in case of RGA? YATA is delta-state CRDT with a fairly low number of restrictions regarding its replication protocol - at least when we compare it to a reliable causal broadcast requirements of their operation-based counterparts. In order to correctly place inserts send out of order, sometimes we may need two pointers instead of just one.
Implementation
Here we won't touch all of the crazy optimizations that Yjs made - we'll discuss them other time - instead we'll focus on being succinct. We'll cover a code, which full working snippet can be found here.
In the introduction we've already discussed the basics of metadata carried over by insert operations, now it's the time to express them in code.
type ID = (ReplicaId * uint64)
type Block<'t> =
{ Id: ID // unique block identifier
OriginLeft: Option<ID> // left neighbor at moment of original insertion
OriginRight: Option<ID> // right neighbor at moment of original insertion
Value: Option<'t> } // value stored in a block, None if tombstoned
member this.IsDeleted = Option.isNone this.Value
type Yata<'t> = Block<'t>[]
Our core unit of composition is Block type. We can simply represent a Yata collection in terms of array, where blocks are laid out in their read order. This makes materialization to our user-readable view very simple:
let value (array: Yata<'t>) : 't[] =
array |> Array.choose (fun block -> block.Value)
Next we're going to define two operations: insertion and deletion at a given index. We'll start with insert. It's very easy. First we need to map user defined index into actual index inside of our Yata collection - since we're keeping deleted blocks around, these two may not be equivalent. Then we obtain IDs of its neighbors (if they exist). Finally we're creating a new block and inserting it at mapped index.
let insert replicaId index value (array: Yata<'t>) : Yata<'t> =
// find actual index in an array, without skipping deleted blocks
let i = findPosition index array
// try to get IDs of left and right neighbors
let left = array |> getBlock (i-1) |> Option.map (fun b -> b.Id)
let right = array |> getBlock i |> Option.map (fun b -> b.Id)
// get the last known sequence number for a given replica
// and increment it
let seqNr = 1UL + lastSeqNr replicaId array
let block =
{ Id = (replicaId, seqNr)
OriginLeft = left
OriginRight = right
Value = Some value }
Array.insert i block array
Deletions are even more straightforward - all we need to do is to map user index with regard to tombstones to find a correct block and remove its value:
let delete (index: int) (blocks: Yata<'t>) : Yata<'t> =
let i = findPosition index blocks
let tombstoned = { blocks.[i] with Value = None }
Array.replace i tombstoned blocks
Merging
Merges are a little bit more complicated. Why? Left and right origins - the very same thing that protects us from interleaving issues - build a dependency chain that will complicate merging process. In order to safely resolve any potential conflicts, that may have appeared in result of concurrent block insertion, we use left and right origins as a reference points. That mean, they must have been there first.
When we're going to do merges we also need to remember about existing blocks that have been tombstoned - we only recognize them by absence of their value. Thankfully, once a block is deleted, it's not reintroduced again: inserting the same value at the same index is still a separate insert operation.
let merge (a: Yata<'t>) (b: Yata<'t>) : Yata<'t> =
// IDs of the blocks that have been tombstoned
let tombstones = Array.choose (fun b -> if b.IsDeleted then Some b.Id else None) b
let mutable a =
a // tombstone existing elements
|> Array.map (fun block ->
if not block.IsDeleted && Array.contains block.Id tombstones
then { block with Value = None } // mark block as deleted
else block
)
// IDs of blocks already existing in `a`
let mutable seen = a |> Array.map (fun b -> b.Id) |> Set.ofArray
let blocks =
b
// deduplicate blocks already existing in current array `a`
|> Array.filter (fun block -> not (Set.contains block.Id seen))
let mutable remaining = blocks.Length
let inline isPresent seen id =
id
|> Option.map (fun id -> Set.contains id seen)
|> Option.defaultValue true
while remaining > 0 do
for block in blocks do
// make sure that block was not already inserted
// but its dependencies are already present in `a`
let canInsert =
not (Set.contains block.Id seen) &&
(isPresent seen block.OriginLeft) &&
(isPresent seen block.OriginRight)
if canInsert then
a <- integrate a block
seen <- Set.add block.Id seen
remaining <- remaining - 1
a
What's easy to miss here is a small integrate function call - it's in fact the heart of our conflict resolution algorithm:
let private integrate (array: Yata<'t>) (block: Block<'t>) : Yata<'t> =
let (id, seqNr) = block.Id
let last = lastSeqNr id array
if last <> seqNr - 1UL
// since we operate of left/right origins we cannot allow for the gaps between blocks to happen
then failwithf "missing operation: tried to insert after (%s,%i): %O" id last block
else
let left =
block.OriginLeft
|> Option.bind (indexOf array)
|> Option.defaultValue -1
let right =
block.OriginRight
|> Option.bind (indexOf array)
|> Option.defaultValue (Array.length array)
let i = findInsertIndex array block false left right (left+1) (left+1)
Array.insert i block array
Based on the left and right origins of the block, we can establish a boundaries between which it's safe to insert a new block eg. if originally block was inserted at index 1, it's left and right origins prior to insertion were are positions 0 (left) and 1 (right). However as blocks can be inserted in the same place at different times on different replicas, the window between left and right origins may have grown. To resolve total order of blocks inserted within that window, we're use following function:
let rec private findInsertIndex (array: Yata<'t>) block scanning left right dst i =
let dst = if scanning then dst else i
if i = right then dst
else
let o = array.[i]
let oleft = o.OriginLeft |> Option.bind (indexOf array) |> Option.defaultValue -1
let oright = o.OriginRight |> Option.bind (indexOf array) |> Option.defaultValue array.Length
let id1 = fst block.Id
let id2 = fst o.Id
if oleft < left || (oleft = left && oright = right && id1 <= id2)
then dst
else
let scanning = if oleft = left then id1 <= id2 else scanning
findInsertIndex array block scanning left right dst (i+1)
What this piece does is to check if there are other blocks that were potentially inserted concurrently at the same position. If so, we're going to compare the unique identifiers of each peer so that inserts made by peers with higher IDs will always be placed after peers with lower IDs.
This is in essence very similar to RGA conflict resolution algorithm (in case of concurrent inserts at the same position shift element to the right if its contender had lower peer id) with one difference:
- RGA block ID uses a single globally incremented counter. A right shift stop condition is: until sequence number of a right-side neighbor's ID is lower than current block's. This has sense, as globaly incremented sequence number means that only concurrently inserted blocks can have same or higher sequence numer.
- YATA block ID uses a counter per replica, however here a right shift stop condition is defined explicitly - it's a position of our right origin.
As you might have noticed this implementation doesn't allow for out-of-order deliveries - which puts some restrictions on our replication protocol. Some implementations (like Yjs) solve this by stashing blocks that have arrived before their predecessors and reintegrating them once block's dependencies have been received.
Deltas
Right now we know how to merge entire snapshot of two Yata replicas. However as we mentioned in the past, this approach is not flexible and can introduce heavy overhead - changing one element would require sending entire state to all peers. This is a motivation behind delta-state replication.
On this blog post we also discussed how to exchange deltas efficiently - so that they only carry information not observed by specific peers. But how can we tell, which updates are yet to be replicated? During the CRDTs series on this blog we already presented so called vector clocks and dotted vector versions (if we want to support out of order deliveries, which for simplicity reasons is not the case here) they let us efficiently describe an observed (logical) timeline of a given CRDT structure.
Fortunately there's a 1-1 relation between YATA block IDs and vector clocks. Here all we really need is to aggregate the highest IDs of all blocks in current YATA array:
let version (a: Yata<'t>) : VTime =
a
|> Array.fold (fun vtime block ->
let (replicaId, seqNr) = block.Id
match Map.tryFind replicaId vtime with
| None -> Map.add replicaId seqNr vtime
| Some seqNr' -> Map.add replicaId (max seqNr' seqNr) vtime
) Version.zero
Given such vector clock, we can also easily generate the deltas themselves. All we need to do is to take blocks which sequence numbers are higher that sequence numbers of corresponding vector clock entries. After this we're almost done: we also need to remember that there might be blocks known to remote peer, that have been deleted in the meantime. For this reason we take IDs of tombstoned blocks and pass them over as well.
type Delta<'t> = (Yata<'t> * ID[])
let delta (version: VTime) (a: Yata<'t>) : Delta<'t> =
let deltaArray =
a
|> Array.filter (fun block ->
let (replicaId, seqNr) = block.Id
match Map.tryFind replicaId version with
| None -> true
| Some n -> seqNr > n)
let tombstones =
a
|> Array.choose (fun block ->
if block.IsDeleted then Some block.Id else None)
(deltaArray, tombstones)
While it may look like pushing all tombstoned elements is not really matching what we'd like to expect from delta behavior, in practice they are minor issue:
- Since we only pass identifiers, their size is pretty small.
- Practical implementations may encode tombstoned ranges in very compact notation eg.
A:(1..100)to encode all deleted blocks fromA:1up toA:100.
After describing these details, implementation of delta merges becomes trivial:
let mergeDelta (delta: Delta<'t>) (a: Yata<'t>) : Yata<'t> =
let (delta, tombstones) = delta
merge a delta // merge newly inserted blocks
|> Array.map (fun block ->
if not block.IsDeleted && Array.contains block.Id tombstones
then { block with Value = None } // tombstone block
else block)
Summary
Here, we presented all the basics of YATA algorithm, used for building conflict-free, delta-state indexed sequences. In the future we're going into deep dive through Yjs/Yrs - a libraries which elevate these principles and improve over them to achieve high efficiency.
References
- Yjs - a production-grade implementation of YATA algorithm. It supports a block-wise CRDTs (similar in principle to what we already presented), different data types (like maps or XML elements).
- A reference implementation of several text-editing structures, written in TypeScript.
- Another implementation made by Seph Gentle, which explores variety of different optimizations that can be done to speedup YATA algorithm.
Comments