Distributed systems: partitions

Today we'll talk about topic of resource allocation in distributed systems using partitions. While we mention two common approaches - partitioning by key and hash rings - further down the post we'll focus only on the second. But let's start from asking: what are partitions and what do we need them for?

There are numerous reasons to build distributed systems, common ones we're mention today are:

1. High availability - we want our system to be always online, even in face of failures. Since we cannot realistically promise that machine our service is operating on will never fail, we may want to replicate the same resource to a different instance to provide redundancy.
2. We may want to bring data relevant to users in certain locations to servers that are physically closer to them in order to reduce latency when serving requests, therefore making our product more responsive.
3. In some scenarios we may also want to mitigate risk of running out of resources on a single machine.

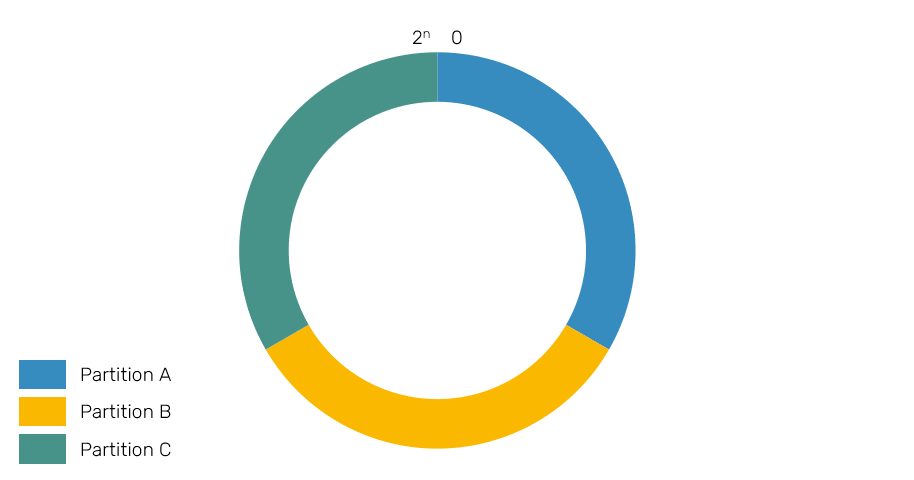
But how are we going to keep track and manage locations of different resource units (entities), if our system may consists of millions or billions of them? In practice we don't - managing every one of them individually would simply be too expensive. Instead we group these entities into partitions (aka. shards), identify them with help of their partition identifiers, and use partition for resource management and location tracking.

Partition keys

Years ago I talked about this topic in context of Akka.NET feature known as Akka.Cluster.Sharding, which allowed for automatic allocation and relocation of your actors among different nodes of your distributed cluster of machines. I won't cover it in detail here, as I already did that on a Petabridge blog (see introduction and deep dive).

tl;dr version is: with this approach each resource (actor) had to explicitly define the shard, in which it lives on. Actors grouped under the same shard were located and managed together by that shard - once created, an actor couldn't change a shard it was assigned to. Similar solution could be found in Azure Table Storage. Since shards could be very different in their volume depending on the number of entities sharing a partition key, it was our responsibility as a system designers to assign shards in a way, so that they won't grow too big.

Consistent hashing

Another approach, popular among projects like Cassandra and Microsoft Orleans is using hashing rings to locate and distribute resources (data rows, grains or entities) across cluster nodes. The basic idea is that instead of using partition keys, we use each entity's own unique id and hash it. Then we use that hash to tell, which partition is responsible for holding that entity. How?

First we organize all possible hash values into so called keyspace - it's a ring with values from 0 to 2^n, where n is the size of returned hash eg. 32-bit, 64-bit or 128-bit are popular cases. We call it a ring because these values are wrapped around the ends eg. range (100, 2] means this range covers all values from 100 (without 100 itself) to 2^32 (for 32-bit keyspace) and from 0 to 2 (including 2). This is important for us, because in this approach we use exclusive ranges of the keyspace to determine the responsibilities of each partition, and unlike in previous approach, partition ranges can change causing migration of their entities.

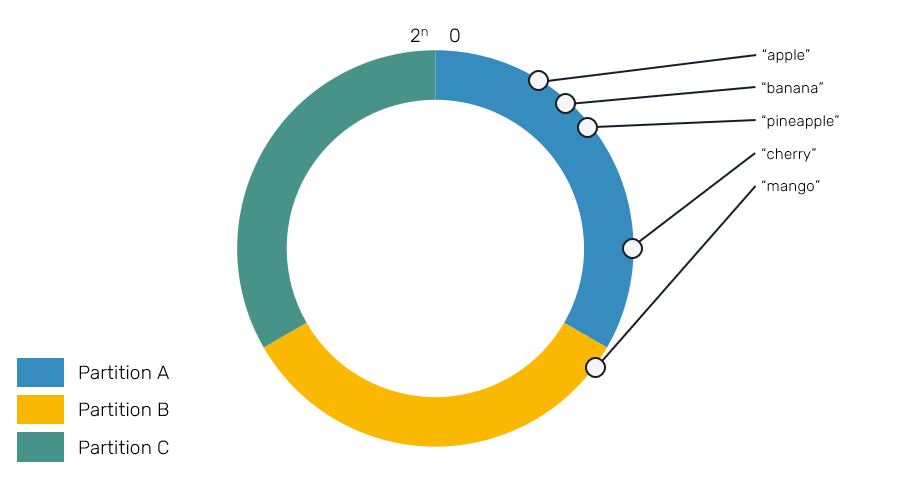
Therefore, whenever we're about to allocate or find a location of an entity, we simply hash its identity and use our hash ring to pick the partition, that entity is supposed to live on. Please take a note, that depending on the actual implementation, partition may be assigned to a single range of hashes or to many disjointed ranges.

There are two algorithms we're about to cover here, but before we do so, let's describe important properties and tradeoffs we want to keep in mind:

• One thing we want is fairness: ideally ranges of responsibilities of each partitions should have the same size. While this doesn't guarantee that resources utilization is fair (we'll talk about it later), it's the next best thing we can aim for.
• Another property is related to rebalancing - once a node is added or removed from the cluster, we may need to migrate resources from other partitions. This means sending potentially huge amounts of data (if we partition eg. disk resources) that can slow down other operations happening on migrating machine. Rebalancing can also take time, so it may be better to scatter it over many machines in small chunks. On the other side we don't want to make this process too noisy for the operating cluster.

We won't cover hash ring partition rebalancing protocol here as it deserves its own post in the future.

Hashing functions

Before we continue, let's get quick recap about consistent hashing functions and their properties. Consistent means, it will always produce the same hash for the same value, regardless of other things like process instance or platform version. For this reason you shouldn't use default object hash code methods, which are common on platforms like .NET/JVM. Also you don't need to (but can) use secure hashing algorithms like SHA, since security usually is not a concern here, while speed is a more welcome property.

Some of the popular (in 2021) functions in use include Murmur3, xxHash and CityHash, which can produce 32, 64 or 128-bit hashes. You may want to checkout a benchmark made by xxhash creators, comparing performance of various hashing algorithms.

When we talked about explicit partition key assignment approach we mentioned about risk of uneven assignment of entities, resulting in some of the partitions being much bigger than others. Since in hash ring approach paritions can scale their ranges, this shouldn't be a problem, right? Wrong. It's still may be an issue, but it's more subtle as it's related to our hashing function: depending on the values of entities identifiers being subject to hashing, it may turn out that their hashes will all be places relatively close on each other on the key space:

This is also why you probably don't want to invent your own hashing algorithm - the ones that we've mentioned above have fairly good distribution and I'd recommend using them unless you really know what you're doing. If you want to read more about how to evaluate hashing functions, I can recommend this thread.

Consistent hash ring

The code snippets presented here are just fragments from the full implementation, which you can find here.

Once we covered the basics (sic!), let's start from writing the most naive version of hash ring - consistent hash ring. It has pretty simple structure:

type ConsistentHashRing =
  { range: RingRange // range current partition is responsible for
    hash: int        // hash of `myself`
    myself: string   // unique identifier of current partition 
    partitions: (int* string)[] }

The last field (partitions) describes the ranges of other known partitions in the system, sorted in hash order eg. array:

[|
  (5, "A")
  (10, "B")
|]

Means that partition A owns range (10,5], while B owns (5,10] (you may notice pretty imbalanced range distribution). We assume that our ranges are right side inclusive - so for this configuration value with hash 5 will go to A. This behaviour is against common intuition of ranges in languages like C#, F# or Rust, but it's consistent with how most of the distributed systems work.

With the explanation above, our partition resolution function should be quite simple to grasp. We simply pick first partition with range containing searched hash:

 let tryFindByHash hash ring =
   let first = Array.tryHead ring.partitions |> Option.map snd
   ring.partitions
   |> Array.tryPick (fun struct(h, p) -> if h >= hash then Some p else None)
   |> Option.orElse first // wrap around the int overflow

Next, we need to consider case when our cluster gets resized - hash rings wouldn't be useful if they didn't acknowledge the fact that cluster can loose or gain new nodes capable of hosting resources. Here we simply compute hash of new partition and insert it in hash sort order.

let add partition ring =
  let hash = hash partition
  if ring.partitions |> Array.exists (fun (h,_) -> h = hash) then ring
  else
    let selfIdx = ring.partitions |> Array.findIndex (fun (_,v) -> v = ring.myself)
    let idx = 1 + (ring.partitions |> Array.tryFindIndexBack (fun (h, _) -> h < hash) |> Option.defaultValue -1)
    let partitions = Array.insert idx (hash, partition) ring.partitions
    let ring = { ring with partitions = partitions }
    if selfIdx >= 0 then
      if selfIdx = idx || selfIdx = 0 && idx = partitions.Length - 1 then
        // update range of current partition
        { ring with range = Continuous (hash, ring.hash) }
      else ring
    else ring

Inversely partition removal removes that entry:

let remove partition ring =
  let removeIdx = ring.partitions |> Array.findIndex (fun (_,p) -> p = partition)
  if removeIdx >= 0 then
    let partitions = Array.removeAt removeIdx ring.partitions // remove partition
    let ring = { ring with partitions = partitions }
    let selfIdx = ring.partitions |> Array.findIndex (fun (_,p) -> p = ring.myself)
    let wasPredecessor = removeIdx = selfIdx || (selfIdx = 0 && removeIdx = partitions.Length)
    if wasPredecessor then
      // update range of current partition
      let range =
        if partitions.Length = 1 then RingRange.full
        else
          let predecessorIdx = Math.Min(Math.Max(0, selfIdx - 1), partitions.Length - 1)
          let struct(predecessorHash, _) = partitions.[predecessorIdx]
          Continuous (predecessorHash, ring.hash)
      { ring with range = range }
    else ring
  else ring

In both cases we additionally update current ring's responsibility range (with respect to hash range overflowing over int.MaxValue). It's useful in case when we need to notice that we need to handover some entities to another partition.

You may notice that adding new node doesn't resize ranges of all nodes. Instead, it takes over its piece of keyspace from the range of its right neighbor:

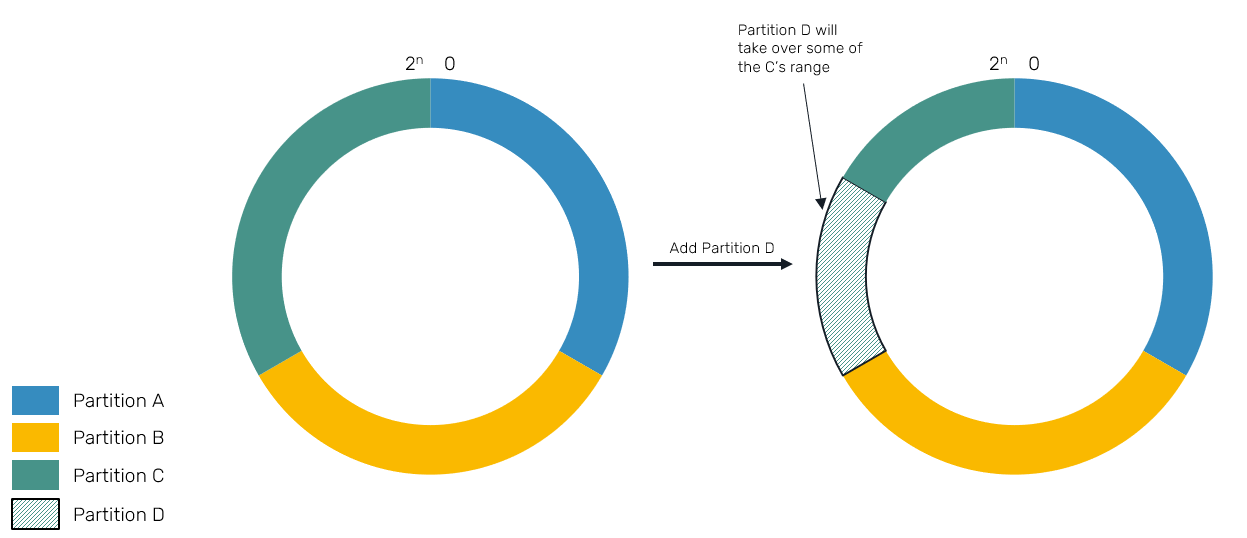
This is not an ideal scenario - at the beginning we mentioned fairness of partition range distribution and sharing the costs of rebalancing. We may notice that this naive implementation is not perfect in any of these cases:

• Insertion of new partition may assign it only a slice of other partition. This is recursive property: in worst case, adding 2nd, 3rd.. Nth partition will result in following partitions taking 1/2, 1/4.. 1/2^(N-1) keyspace. That's rather unfair compared to 1/N share we strive for. But don't worry: in practice it's very unlikely to happen.
• Range changes affect only 2 partitions at the time, resulting in one of them giving up huge portion of resource space to another. Imagine that one of our partitions had 2TB of data, and in result of attaching new node, it now may have to send 1TB of data to it... while still serving user requests! This may add pressure to our node, result in potential request timeouts, latency spikes or cause rebalancing to take a long time to complete.

Virtual Bucket Ring

Another approach, we're going to implement is known as virtual bucket ring. The idea is simple: given some configured factor N, everytime we're about to add new node we're not going to add single entry like in the case of consistent hash ring, but instead we'll create N buckets scattered all over keyspace. These entries will again slice existing ranges, but on much more sparse area of keyspace:

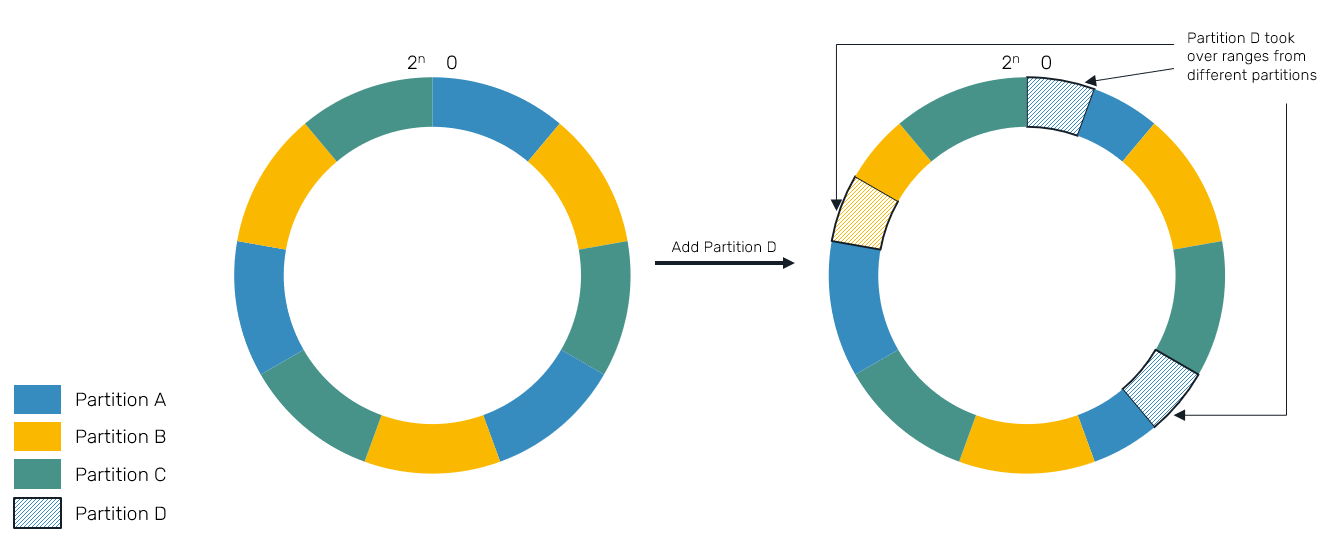
You can see, that our partition range is no longer a single pair of boundaries in this scenario. Instead, each partition may be responsible for many fragments of keyspace.

We'll start our implementation from defining our hash ring structure, which on first glance looks super similar to consistent hash ring:

type VirtualBucketRing =
  { hash: int
    myself: string
    range: RingRange
    N: int // number of buckets inserted per partition
    buckets: Map<int,string> } // sorted array

In fact it could be implemented in the same way, we're just using map instead of array to make some operations easier. Finding partition for a given hash also looks pretty much the same as in case of ConsistenHashRing:

let tryFindByHash hash ring =
  let first = ring.buckets |> Seq.tryHead |> Option.map (fun e -> e.Value)
  let found = ring.buckets |> Seq.tryPick (fun e -> if e.Key >= hash then Some e.Value else None)
  found |> Option.orElse first  // wrap around to first element

Now, at the beginning we said that adding new partition will result in generating N new buckets (each bound by some hash range). How do we get all these hashes from? A common technique is to create hashes by attaching N unique suffixed to hashed value:

let private uniformHashes value count =
  let hashes = Array.zeroCreate count
  for i=0 to Array.length hashes - 1 do
    let suffix = string i
    hashes.[i] <- hash (value + suffix)
  hashes

Now let's consider adding new node:

let add partition ring =
  if Map.exists (fun k v -> v = partition) ring.buckets then ring
  else 
    let hashes = uniformHashes partition ring.N
    let buckets = hashes |> Array.fold (fun buckets hash ->
      match Map.tryFind hash buckets with
      // in case of partition collision resolve conflict
      // using partition id seniority
      | Some other when partition > other -> buckets 
      | _ -> Map.add hash partition buckets) ring.buckets
    let range = update ring.myself buckets
    { ring with range = range; buckets = buckets }

We simply create N new buckets and insert them into our array - having in mind that with a huge number of buckets some collisions are not impossible. Again removal is all about removing entries which we previously added:

let remove partition ring =
  if Map.exists (fun k v -> v = partition) ring.buckets then
    let hashes = uniformHashes partition ring.N
    let buckets =
      hashes
      |> Array.fold (fun buckets hash ->
        // check for bucket hash collisions
        match Map.tryFind hash buckets with
        | Some p when p = partition -> Map.remove hash buckets
        | _ -> buckets) ring.buckets
    let range = update ring.myself buckets
    { ring with range = range; buckets = buckets }
  else ring

In both cases we again want to update our current ring range, but since it's fragmented, it's a little bit harder. What we essentially do, is taking modified buckets map with pairwise entries (last pair is wrapping (lastBucket, firstBucket]), checking which of them belong to current partition and combining them together:

let private update partition (buckets: Map<int,string>) =
  let mutable e = (buckets :> IEnumerable<_>).GetEnumerator()
  let ranges = ResizeArray()
  if e.MoveNext() then
    let first = e.Current
    let mutable current = first
    
    while e.MoveNext() do
      let next = e.Current
      if next.Value = partition then
        ranges.Add (current.Key, next.Key)
      current <- next
      
    if first.Value = partition then // keyspace overlap
      ranges.Add (current.Key, first.Key)
      
    RingRange.create (ranges.ToArray())
  else RingRange.full

Ultimately this implementation was not excessively harder than ConsistentHashRing - the major trick was to generate a configurable number of ranges instead of blindly using a single one, which lets us involve more partitions, spreading the range more evenly.

Now, what value should N have? There's not a single formula for that, so let's build some intuition. First this value needs to be the same on all nodes at all times. If we're about to create N new buckets each time we add new node, it means that up to N other partitions may take part in rebalancing process. This will spread the load more fairly - which is good - but there's more to it:

• There's no guarantee that N partitions will be affected. Sometimes bucket ranges may collide. Other times, two buckets will land next to each other, still on the same partition (although hash functions are good at avoiding that case). So, N is just an upper bound for partitions to take part in resizing process.
• Since N new buckets are created for every partition added, setting it to a big number may negatively affect in-memory size of our data structure.
• If N is much bigger than final designed cluster size, it's pretty much useless. More over, it may cause problems, since...
• ... if we're about to involve many partitions in rebalancing process, we need to be sure they all are online until the process ends, which is not so obvious. One of the desired properties of distributed systems is ability to work even when individual nodes may crash. The greater number of nodes creating our cluster, the higher probability of some of them failing randomly.

Final notes

In this blog post we quickly described what do we use partitions for in distributed systems and what kinds of partitioning are out there. We also covered two of the most basic and most popular algorithms for building hashing rings.

If you're interested in other hashing data structures, you may be interested in Sliding Random Hash Ring article on InfoQ, which describes some of the trade-offs we mentioned with new approach. It also covers ideas like assigning weights to partitions, useful eg. when some machines have higher resource capabilities than others. If you're interested in how to implement it, you can read the open source implementation in Pony language here.